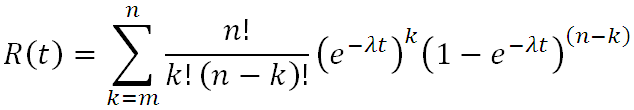


Return to Redundancy Calculator
The tool provides the following capabilities:
1. Reliability Function
It provides the reliability function, R(t), based on the redundancy level entered. R(t) is derived using the most
general R(t) equation for "m of n Must Be Working", for "n" fully energized identical parallel units, as shown on page 160 of the
Reliability Toolkit: Commercial Practices Edition (Ref. 2).
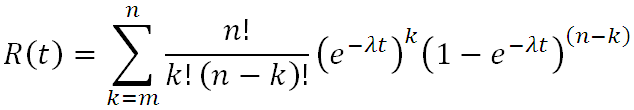
It uses Gauss Integration to numerically evaluate the following equation, thus avoiding the approximation formula
described by McGregor (Ref. 6), and providing greater accuracy in some situations,
specifically when the failure rate is not small compared to the repair rate. For McGregor's approximation formula to be accurate the failure rate should be much smaller than the repair rate
(λ<<μ). If corrective maintenance
is significantly delayed (e.g., λ>0.1μ), then the approximation formula will result in a more conservative estimate of effective MTBF.
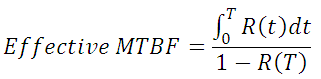
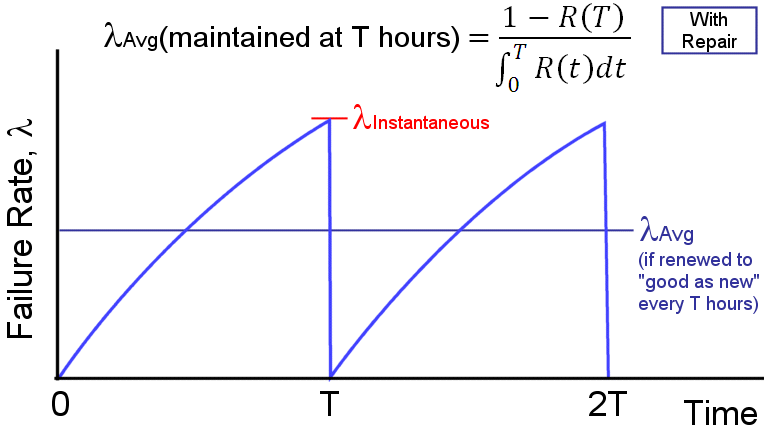
where T is the maintenance interval (i.e., the system is restored to "as good as new" every T hours). The effective failure rate is the reciprocal of the effective MTBF. The following figure
shows the concept of effective, or average failure rate, over time as the system is renewed every T hours. The instantaneous system failure rate, which increases over time as redundant
units fail, is shown at time T. The instantaneous failure rate increases over time as redundant units fail and less fault tolerance remains.
It calculates mean time to failure (MTTF) using Gauss Integration:
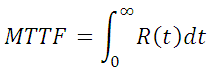
It also allows for the use of the Weibull failure distribution, thus providing greater accuracy if failures do not occur randomly over time (i. e., non-constant unit failure rate).
It also allows for the output of the derived reliability function, R(t), as a Microsoft Excel formula, thereby allowing for manipulation and plot generation within Microsoft Excel.

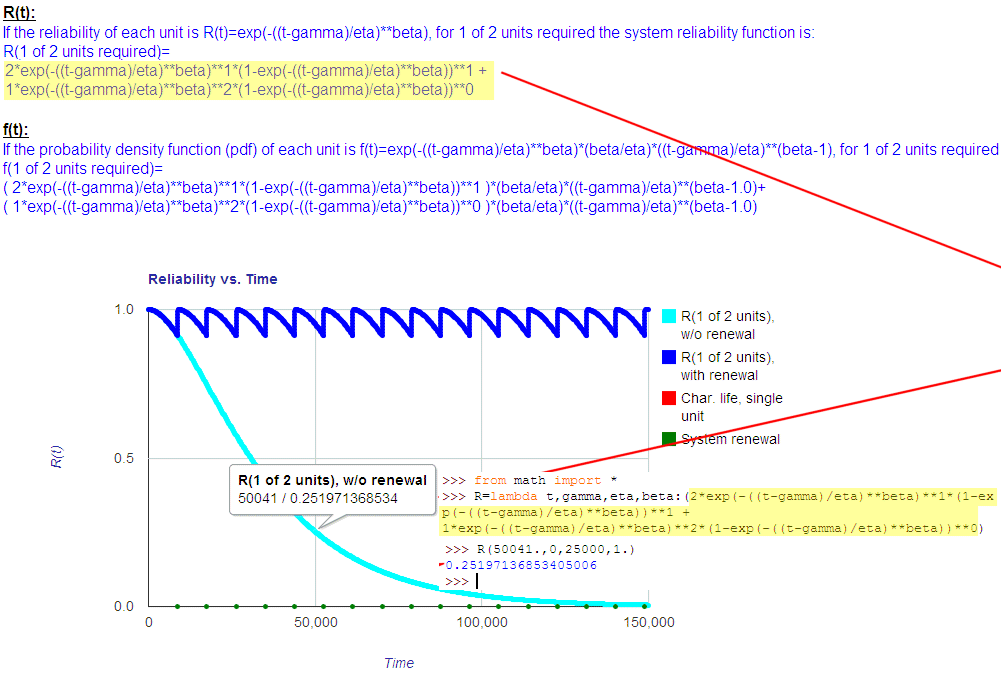
It also allows for the output of the derived reliability function, R(t), as a text string that can be directly used in a Python programming language lambda function, thereby allowing for further customized reliability modeling
within the Python programming environment. For example, the following picture shows text output highlighted in yellow. In the Pythion shell shown on the right, this text is pasted into a Python lambda function
that takes inputs (in this example) of t, gamma, eta and beta; thereby, allowing easy computation of reliability for any combination of these inputs. Python is available from http://python.org/, or an on-line version
of the Python shell is available by clicking the calculator icon in the lower right-hand corner of this page.
Toolkit Home
Comments/Questions:

reliabilityanalytics.com