Reliability Analytics CorporationPowered by Google App Engine

Reliability and Effective Failure Rate of "n" Active Redundant Units, with "m" Required for Success

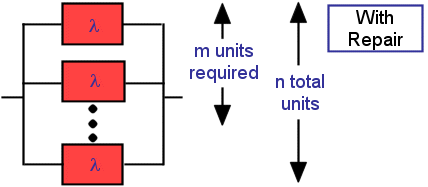
This tool calculates the reliability function and effective failure rate for "m of n" active on-line units. It includes the capability to model units failing in accordance with either the exponential or Weibull failure distributions. For comparison purposes, it also provides options to output reliability metrics associated with non-repairable scenarios. It is similar to this tool, but is more comprehensive in that it uses numerical integration to compute the effective mean time between failure (MTBF), sometimes referred to as the mean time between critical failure (MTBCF). In addition, it handles non-constant unit failure rates using the Weibull distribution and provides graphing capability. For additional details, click here.

See this page for additional details on time inputs (T) for system restoration.

Reliability Block Diagram:


Reliability Block Diagram showing n active units with m units required for success

Calculation Inputs:

1. Number of units required for mission success (m):
2. Total number of active on-line units (n):
3. Maintenance interval for system renewal (T), hours:

4.

4a. If Exponential Distribution was selected in #4, then enter:


4b. If Weibull Distribution was selected in #4, then enter:
Shape parameter, beta (β):
Characteristic life, eta (η):

The Weibull distribution can be made to fit many other life distributions by adjusting the shape parameter, beta (β). The characteristic life, eta (η), also sometimes called scale parameter, is the point where 63.2% of the population will fail, regardless of the underlying failure distribution (value of beta). A beta value of 1.0 is equivalent to the exponential distribution and a value of 3.5 approximates the normal distribution.


5. Decimal places:

6. Format for R(t) output:

7. Options:

Plots
R(t)
f(t)
h(t)

Without renewal
With renewal ( renewal interval)
Single unit
Zoom plot

Title:

Additional outputs:
R(T)
Instantaneous MTBF at T
Series MTBF
MTTF





Featured Reference:

Reliability Engineering
Reliability Engineering


Toolkit Home

Comments/Questions:
Feedback
Reliability Analytics Corporation
reliabilityanalytics.com

References:

  1. United States Air Force Rome Laboratory Reliability Engineer's Toolkit (1993).
  2. Reliability Toolkit: Commercial Practices Edition, United States Air Force Rome Laboratory and the DoD Reliability Analysis Center, (1995).
  3. MIL-HDBK-338, Electronic Reliability Design Handbook.
  4. Klion, Jerome, A Redundancy Notebook, Rome Air Development Center, RADC-TR-77-287, December 1987.
  5. Reliability Modeling and Prediction, MIL-STD-756B, November 1981.
  6. McGregor, Malcolm A., Approximation Formulas for Reliability with Repair, IEEE Transactions on Reliability, Volume R-12, Number 4, December 1963.
  7. Bazovsky, Igor, Reliability Theory and Practice.
  8. O'Connor, Patrick, D. T., Practical Reliability Engineering.
  9. Barringer, Paul, Barringer & Associates, Inc., database of typical Weibull shape and characteristic life parameters (wdbase), Feb. 22, 2010 (no longer available online).
  10. http://en.wikipedia.org/wiki/Gaussian_quadrature