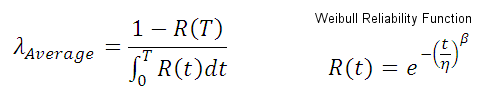This tool can be used to make average failure rate estimates (or MTBF) for items that do not exhibit a constant failure rate, such as for mechanical components. These types of components often have a reliability metric quoted in terms of L10% life, the point in time where 10% of a population of items is expected to fail. Given a Weibull shape parameter (β),
Lx% life and a maintenance interval for item renewal, T, when the item is assumed to be restored to "as good as new," this tool estimates an average item failure rate and MTBF.
The average failure rate is calculated using the following equation (Ref. 1), where T is the maintenance interval for item renewal and R(t) is the Weibull reliability function
with the appropriate β and η parameters. The characteristic life (η) is the point where 63.2% of the population will fail.
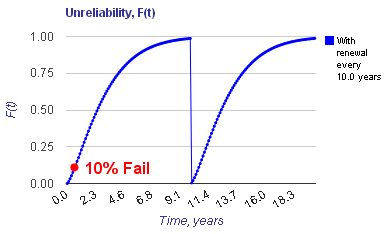
Example: A ball bearing has a Weibull shape parameter of 1.3 and an L10% life of 5,000 hours (0.6 years) as shown on the F(t) chart below. What is the average failure rate for the bearing? If the bearing is scheduled for
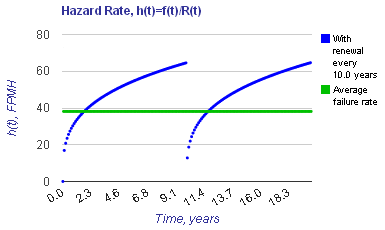
preventive maintenance replacement every 10 years, the hazard rate varies from a lower value of zero at "time zero" to an upper bound of 64 failures per million hours (FPMH) for bearings that survive to the 10 year point. The average failure rate for a population of these bearings is estimated
to be approximately 38 FPMH, as depicted by the green line shown in the hazard rate plot below.
Toolkit Home
Comments/Questions:
reliabilityanalytics.com