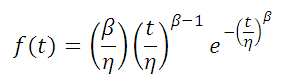 Probability Density Function
Probability Density Function
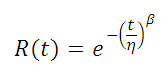 Reliability Function
Reliability Function
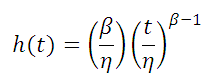 Hazard Rate
Hazard Rate

The Weibull distribution can be used to model many different failure distributions.
Given a shape parameter (β) and characteristic life (η) the reliability can be determined at a specific point in time (t).
The two-parameter Weibull distribution probability density function, reliability function and hazard rate are given by:
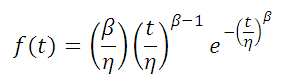 Probability Density Function
Probability Density Function
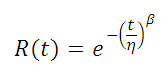 Reliability Function
Reliability Function
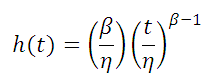 Hazard Rate
Hazard Rate
The characteristic life (η) is the point where 63.2% percent of the population will have failed, regardless of the shape parameter (β).
The following shape parameter characteristics are noted:
β = 1.0 : Exponential distribution, constant failure rate
β = 3.5 : Normal distribution (approximation)
β < 1.0 : Decreasing failure (hazard) rate
β > 1.0 : Increasing failure (hazard) rate