

Weibull Analysis Background Information
The resulting analysis provides estimates for the Weibull shape parameter, β, and characteristic life, η. The reliability and hazard rate can be determined
estimated at a specific point in time (x) using the derived β and η.
Using these parameters, the Weibull distribution can then be used to model many different failure distributions.
The two-parameter Weibull distribution probability density function, reliability function and hazard rate are given by:
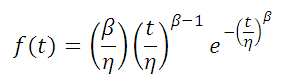 Probability Density Function
Probability Density Function
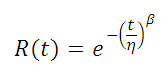 Reliability Function
Reliability Function
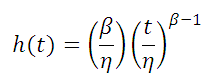 Hazard Rate
Hazard Rate
A three-parameter Weibull Distribution also includes a location parameter, sometimes termed failure free life. For these cases, t in the above above equations is replaced by t-δ.
The characteristic life, η, is the point where 63.2% percent of the population will have failed. This is true regardless of the shape parameter (β) chosen.
The following shape parameter characteristics are noted:
β = 1.0 : Exponential distribution, constant failure rate
β = 3.5 : Normal distribution (approximation)
β < 1.0 : Decreasing failure (hazard) rate
β > 1.0 : Increasing failure (hazard) rate
Median ranks are calculated using the following equation.
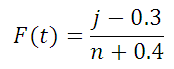 Median Rank Equation
Median Rank Equation
where:
j is the failure order
n is the sample size
Data that contains non-failed items is termed "censored," or "suspended" test data. For this type of data adjusted ranking, or ordered points, are calculated and used to calculate F(t), the cumulative fraction failed. This modified order is then used
for j in the above median rank equation. The column labled Increment in the table is calculated using the following equation.
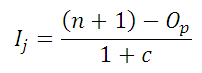 Increment Equation
Increment Equation
where:
Ij is the increment for point j.
n is the total number of records, both failures and censored items.
Op is the order of the previous point, or record.
c is the number of remaining points, including the current point.
The order of each point, Oj, is the order of the previous point, Op, plus Ij calculated according to the above equation. These calculations are shown for each
point in the table columns labeled Increment and Order in the calculation results.
The calculation inputs are show units of "hours," but any life metric (cycles, years, miles, etc.) can be used as long as there is consistency among the inputs.
Toolkit Home
Comments/Questions:


reliabilityanalytics.com
References:
- MIL-HDBK-338, Electronic Reliability Design Handbook.
- Nelson, Wayne, Applied Life Data Analysis
- Dodson, Bryan, The Weibull Analysis Handbook.
- Dodson, Bryan, The Weibull Analysis Handbook.
- Abernethy, Robert, The Weibull Analysis Handbook.
- Bazovsky, Igor, Reliability Theory and Practice.
- O'Connor, Patrick, D. T., Practical Reliability Engineering.
- http://en.wikipedia.org/wiki/Weibull_distribution
- http://en.wikipedia.org/wiki/Maximum_likelihood
- Weibull Distribution, NIST Engineering Statistics Handbook .
- Khan Academy, Probability density functions for continuous random variables..
- Barranger, Paul, See http://www.barringer1.com/wdbase.htm for a database of typical Weibull shape and characteristic life parameters.
- http://reliawiki.org/index.php/Weibull_Distribution_Examples
- Kececioglu, Dimitri, Reliability & Life Testing Handbook.
Copyright © 2010 - 2023 Reliability Analytics Corporation
Privacy Policy
All content and materials on this site are provided "as is" Reliability Analytics makes no warranty, express or implied, including the warranties of merchantability and fitness for a
particular purpose; nor assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed;
nor represents that its use would not infringe privately owned rights.
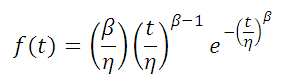 Probability Density Function
Probability Density Function
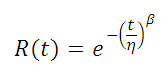 Reliability Function
Reliability Function
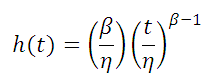 Hazard Rate
Hazard Rate

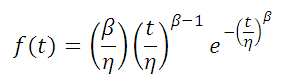 Probability Density Function
Probability Density Function
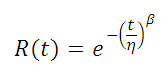 Reliability Function
Reliability Function
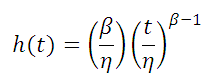 Hazard Rate
Hazard Rate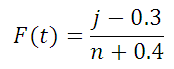 Median Rank Equation
Median Rank Equation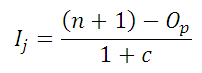 Increment Equation
Increment Equation
