This tool implements calculations for the conditional Weibull distribution found on pages 69-70 of Nelson (reference 1) and is pre-filled with example data from Nelson to calculate the remaining expected life for 6.5 year-old windings to be 7.1 years, given a Weibull shape parameter of β = 2.0 and a winding characteristic life of η = 13 years. The tool is intended to provide estimates for questions such as:
1. Given that an item has survived for 6.5 years, what is the expected mean age at failure? To answer this question, fill in inputs one, two and three below. The calculation uses the following equation (ref. 1) and makes us of the “lower” incomplete gamma function found in the Python mpmath package (ref. 2, 3).
2. Given that an item has survived for 6.5 years, what is the expected median age at failure? To answer this question, fill in inputs one, two, three and six below.
The percentile life is calculated using the following equation (for median life, P=0.5, for 10% life, P=0.10).
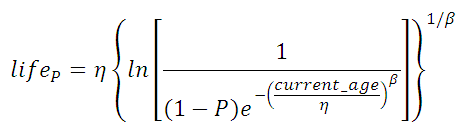
3. Given that an item has survived for 6.5 years, what is the probability of survival to an age of 13 years old? To answer this question, fill in inputs one through four below.
Given that an item that has survived to an age of
current_age, the cumulative probability of failure up to some
future_age is given by:
where: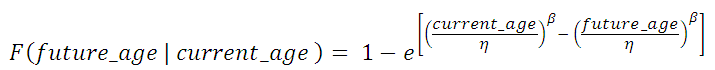
β is the Weibull distribution shape parameter
η is the Weibull distribution characteristic life
