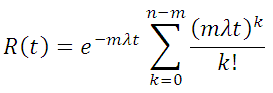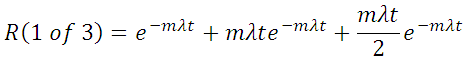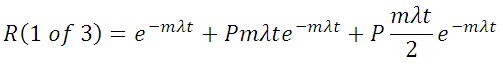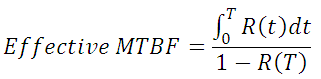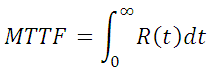Return to Redundancy Calculator
The tool provides the following capabilities:
1. Reliability Function
It provides the reliability function, R(t), based on the redundancy level entered. R(t) is derived using the most
general R(t) equation for "m of n Must Be Working", for "n" fully energized identical parallel units, as shown on page 160 of the
Reliability Toolkit: Commercial Practices Edition (Ref. 2).
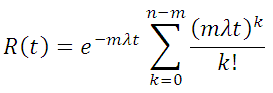
This equation has been further modified to factor in the probability that the switching mechanism works
correctly. Each term in the above summation for k>0 represents one additional failure in the overall system, an thus an additional switching action.
Therefore, each term for k>0 is multiplied by the probability P that the switch will work correctly.
For example, for a system of three units (n=3), with one unit required (m=1) for success and two units that are cold standby spares (n-m=2):
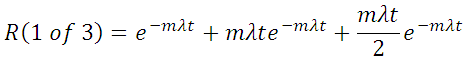
The first term represents the probability of no failures, the second term the probability of exactly one failure (requiring one switching action) and the third term the probability of two failures (requiring a second switching action).
The above assumes perfect switching. If each switching action is imperfect and occurs with probability P, then the overall probability of success is:
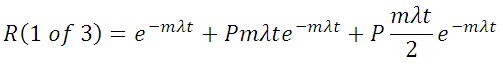
2. Effective MTBF
It uses Gauss Integration to numerically evaluate the following equation.
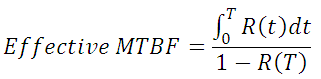
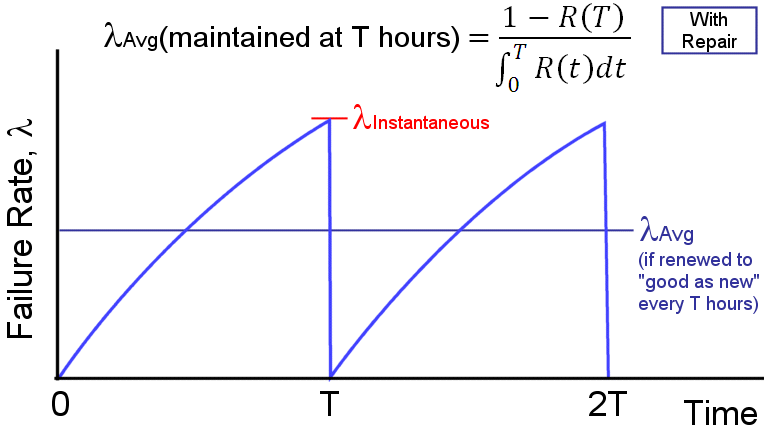
where T is the maintenance interval (i.e., the system is restored to "as good as new" every T hours). The effective failure rate is the reciprocal of the effective MTBF. The following figure
shows the concept of effective, or average failure rate, over time as the system is renewed every T hours. The instantaneous system failure rate, which increases over time as redundant
units fail, is shown at time T. This failure rate increases over time as redundant units fail and less fault tolerance remains.
3. MTTF
It calculates mean time to failure (MTTF) using Gauss Integration:
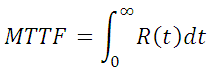
4. Excel Output
It also allows for the output of the derived reliability function, R(t), as a Microsoft Excel formula, thereby allowing for manipulation and plot generation within Microsoft Excel.
5. Text Output
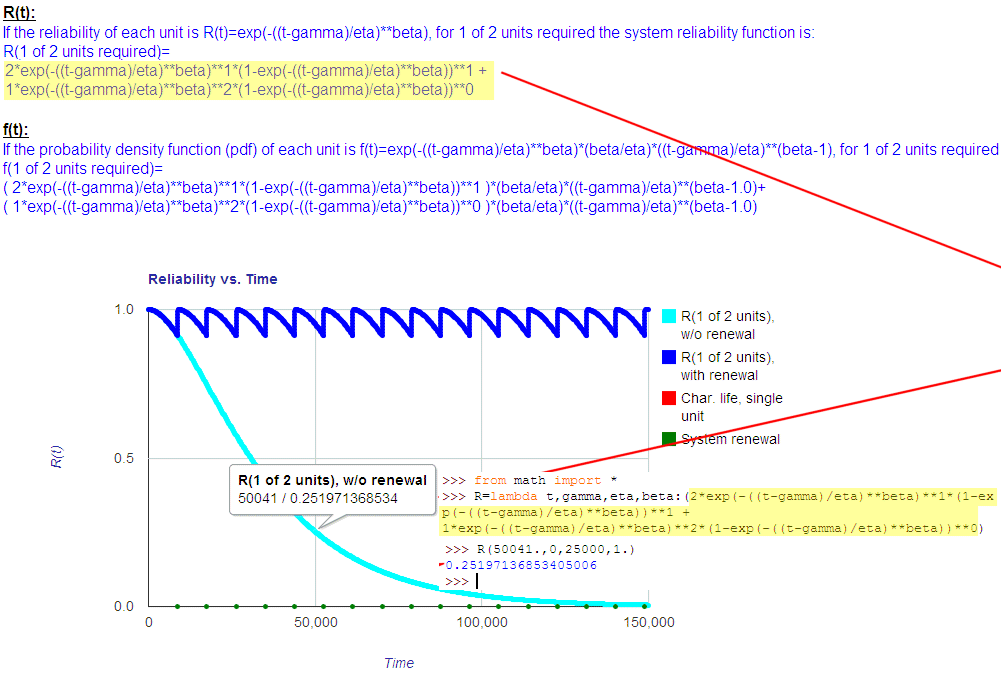
It also allows for the output of the derived reliability function, R(t), as a text string that can be directly used in a Python programming language lambda function, thereby allowing for further customized reliability modeling
within the Python programming environment. For example, the following picture shows text output highlighted in yellow. In the Pythion shell shown on the right, this text is pasted into a Python lambda function
that takes inputs (in this example) of t, gamma, eta and beta; thereby, allowing easy computation of reliability for any combination of these inputs. Python is available from http://python.org/, or an on-line version
of the Python shell is available by clicking the calculator icon in the lower right-hand corner of this page.
Toolkit Home
Comments/Questions:
reliabilityanalytics.com