Sequential Testing: Testing the Mean of a Binomial Distribution

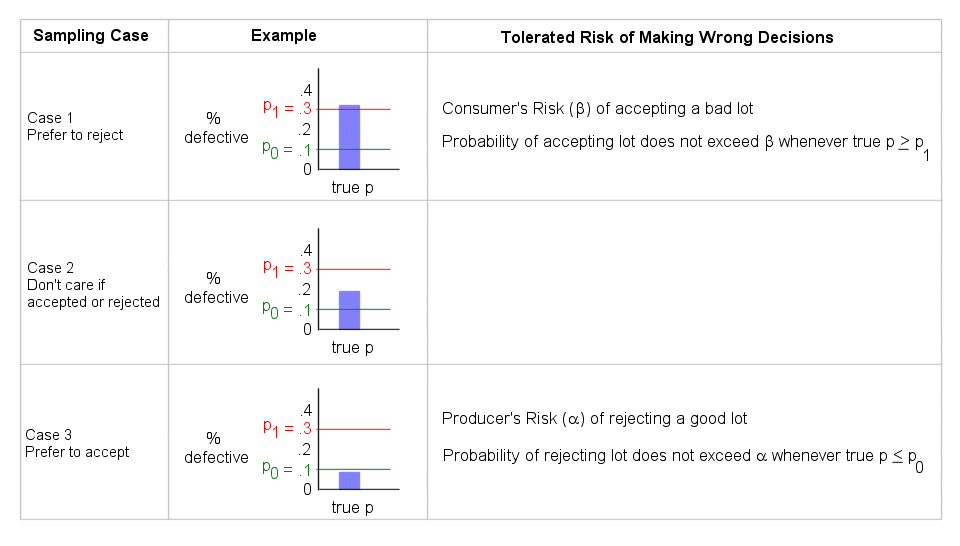
This tool provides the ability to plan a sequential lot acceptance test where each unit is classified into one of two categories, good or defective. It is based on the work of Abraham Wald (Ref. 2). The following shows the possible sampling outcomes and the preferences for test decision outcome. "true p" in the example column below is the true proportion defective in the lot if all units were to be inspected. See reference 2, Chapter 5, "Testing the Mean of a Binomial Distribution (Acceptance Inspection of a Lot Where Each Unit is Classified Into One of Two Categories)" for additional details.

Calculator input parameters are as follows:

• Unacceptable proportion defective (p₁). The probability of accepting the lot does not exceed the consumer's risk (β) whenever the true proportion defective (p) is greater than or equal to p₁.
• Acceptable proportion defective (p₀). The probability of rejecting the lot does not exceed the producer's risk (α) whenever the true proportion defective (p) is less than or equal to p₀.
• Consumer’s risk (β). The consumer’s risk is the probability of accepting a lot with a true proportion defective equal to or greater than the unacceptable proportion defective (p₁). β probability of lot acceptance for Case 1.
• Producer’s risk (α). The producer’s risk is the probability of rejecting a lot with a true proportion defective equal to or less than the acceptable proportion defective (p₀). α probability of lot rejection for Case 3.
• True p. The true proportion defective in the lot if all units were to be inspected.

Tip: To experiment with the test methodology select "simulation" in the chart overlay pull down and vary input parameters (1-4) along with "true p" (input 5C).

Calculation Inputs:

1. Unacceptable proportion defective, p₁ (1 > p₁ > p₀):

2. Acceptable proportion defective, p₀ (0 < p₀ < p₁):

3. Consumers risk (β)3% .1% .5% 1% 2% 3% 4% 5% 7% 10% 15% 20% 25% 30%

4. Producers risk (α)2% .1% .5% 1% 2% 3% 4% 5% 7% 10% 15% 20% 25% 30%

5. Optional:

5A. x axis scale factor 3 5 10 25 50 Table

Chart overlay: Use observed defects entered in 5B Simulate testing using true proportion defective entered in 5C

5B. Number of defects observed (# inspected, # defects observed):
1,0 2,0 3,1 4,1 5,1 6,1 7,1 8,1 9,2 10,2 11,3 12,4 13,4 14,5 15,5 16,5 17,5 18,6 19,6 20,6 21,6 22,7

Above input is:
a. comma separated entry, one per line: # inspected, # defects observed
b. copy/paste two columns from Excel: # inspected    # defects observed
Excel template

5C. Simulation true proportion defective (range: 0 to 1.0): Number of tests:1 2 3 4 5 6 7 8 9 10

Featured Reference:

Reliability Theory and Practice

Toolkit Home

Comments/Questions:


reliabilityanalytics.com

---

References:

1. Bazovsky, Igor, Reliability Theory and Practice.
2. Wald, A., Sequential Analysis.
3. Wald, A. (1945). Sequential tests of statistical hypotheses. Annual Mathematica Statistics. 16, 117-186.
4. http://en.wikipedia.org/wiki/Sequential_analysis

Copyright © 2010 - 2023 Reliability Analytics Corporation

Privacy Policy

All content and materials on this site are provided "as is" Reliability Analytics makes no warranty, express or implied, including the warranties of merchantability and fitness for a particular purpose; nor assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed; nor represents that its use would not infringe privately owned rights.