Reliability Analytics CorporationPowered by Google App Engine

Discrete Event Simulation

The tool is pre-filled with example data based on the reliability block diagram shown below. Click the Calculate button for an example simulation. The tool simulates the failure and repair process for different units, each with an independent failure and repair distribution, using discrete event simulation (Monte Carlo) techniques. It allows for a user defined "watch list" of failure events that result in a "critical" failure. Uses include:

1. Estimating system mean time between critical failure (MTBCF) for a system consisting of units with different failure and repair scenarios.
2. Estimating system operational availability (Ao).
3. Providing graphical visualizations of the overall failure and repair process for individual units, as well as a system of units operating together.
4. Estimating spare part requirements and the impact of different maintenance policies, such as local versus remote spare parts, on Ao and MTBCF.
5. Other custom off-line analyses using the export to Microsoft Excel feature. These can include generating pivot tables of spare part usage and associating cost metrics with failure and repair counts.

The calculation inputs below are prefilled with example data for a hypothetical "system", with a "mission" reliability block diagram (RBD) model as shown below. Fault tolerance exists as shown in the RBD and specified by input #2 below. Only critical failures are assumed to cause system unavailability.

RBD showing essential components required for mission success
The underlying discrete event simulation engine is SimPy (Simulation in Python); which is an object-oriented, process-based discrete-event simulation language for the Python programming language. See references 1-3 for additional details on SimPy, along with reference 7 for information on the underlying random number generator used.

Excel Input Template/Examples

Examples (Blog)

Calculation Inputs:

1. Unit failure/repair characteristics (edit/copy/paste example input to make new entries, or use the Excel template above).

Column 1 entry must be unique, otherwise the failure and restore characteristics for the last entry with the same key (serial number) will be used.
Columns 1, 2 and 3 are required. These are a serial number (i.e., any unique key/name), failure characteristic and restoration characteristic, respectively.
Column 4 is item description and column 5 part number. Both of these are optional, but may be useful if exporting results to Excel and performing post simulation analysis (e.g., how many failures for a given part number).

Failure characteristic 800,200,n means a normally distributed life of 800 hours, with a standard deviation of 200 hours.
Restoration characteristic 168,48,n means a normally distributed restore time of 168 hours, with a standard deviation of 48 hours.
Failure characteristic 20000,e means an MTBF of 20,000 hours, with an exponential failure distribution.
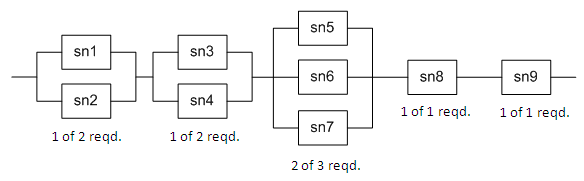
Repair time for sn6 is exponentially distributed with a mean of 48.
Failure characteristic 1000,3.5,w means a Weibull characteristic life of 1000 hours, with a Weibull shape parameter of 3.5.
Single number entries mean exact times. snA "fails" every 2,190 hours (exactly) and is restored in exactly 1 hour.

 unique SN | failure characteristic | repair characteristic | desc. (optional) | part no. (optional)

2. Failure combinations that result in a critical failure (enter one combination per line, with each unit serial number separated by a comma).

This input is optional. It can be used to define a "watch list" for various combinations of failure events. Only SNs previously defined in box #1 above are meaningful input. After each simulated failure event, each set of items (one set per line below) is compared to the current list of items in a failed state. If the set of items listed on a line below is a subset of the current set of failed items, then a "critical failure" is tallied. This tool (option 1d) may be helpful to enumerate all possible states for a given list of serial numbers, which can be exported to Excel, specific combinations selected, and pasted into the box below.

 one set per line


3. Regularly scheduled preventive maintenance (PM) interval (enter one unique serial number per line, followed by a comma and the scheduled maintenance interval (hours). If restoration is only performed at scheduled intervals, add the word "delayed" in the optional third field.).

This input is optional. It can be used to define a regularly scheduled maintenance interval when a specific serial numbered item is restored to "as good as new." For the example input shown below, all units are restored to "as good as new" at the time interval indicated; however, if either of the bearings fail (sn8 or sn9), restoration begins immediately, taking the time defined in box #1 above. If either of the control units fail (sn3 or sn4), restoration is delayed until the next regularly scheduled maintenance, which occurs every 4,000 hours. Only SNs previously defined in box #1 above are meaningful input.

unique SN, scheduled PM interval, delay flag (optional)


4A. Simulation length for each trial (hours):
4B. Number of trials:

5. Seed: Enter the same seed to repeat results, otherwise leave blank. Seed automatically increments by one for each trial.

6. Confidence level:

7. Output options:

If the browser output is truncated, export to Excel.

Output event table for trial number:
Verbose event table description

Unit up/down charts:
Cumulative system failures chart:
System quantity up chart:
Cumulative critical system failures chart:
System mission up/down chart:

User entered data summary
Spare parts usage table
Decimal places (Lg./Sm. #'s):





Featured Reference:

Simulation with Arena
Simulation with Arena


Toolkit Home

Comments/Questions:
Feedback
Reliability Analytics Corporation
reliabilityanalytics.com

References:

  1. SimPy Home Page
  2. Matloff, Norm, University of California at Davis, Dept. of Computer Science, Introduction to Discrete-Event Simulation and the SimPy Language
  3. Matloff, Norm, University of California at Davis, Dept. of Computer Science, A Discrete-Event Simulation Course Based on the SimPy Language
  4. Banks, Jerry, Discrete-Event System Simulation.
  5. Law, Averill, Simulation Modeling and Analysis.
  6. Kelton, W. David, Simulation with Arena.
  7. Python pseudo-random number generator