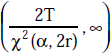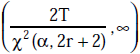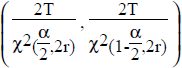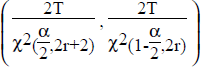If equipment could be tested for infinite time, a "true" mean time between failure (MTBF) could be computed. However, since that is not feasible, it is often desirable to calculate confidence bounds based on far more limited information.
Instead of simply quoting a "point estimate" MTBF, reliability engineers are usually most interested in the lower bound MTBF, for example, to state that "the MTBF is at least 1,800 hours with 90% confidence." As shown in
the picture below, with
little experience (few failures) the upper and lower confidence bands are very wide. For example, with only one failure over 100 hours, the point estimate MTBF is 100 hours, with an upper limit 50%
confidence bound (red line) of approximately 350 hours and a lower 50% confidence bound of approximately 40 hours. As experience increases (more failures), these bands become much tighter.
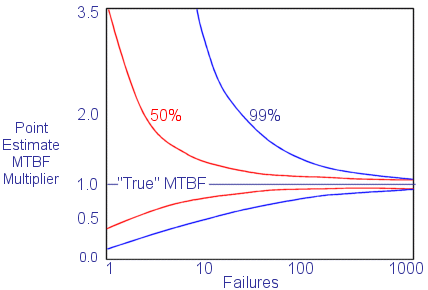
Multiplication Factors for Determining Confidence Levels Based on Number of Failures
Two situations have to be considered for estimating confidence intervals:
1. A test that is run until a pre-assigned number of failures have occurred.
2. A test that is stopped after a pre-assigned number of test hours have accumulated.
The formula for the confidence interval employs the χ 2 (chi-square) distribution.
The general notation used is:
χ 2p,d
where p and d are two constants used to choose the correct χ 2 value.
p is a function of the confidence coefficient.
d is the degrees of freedom, which is a function of the number of failures.
| One Sided (Lower Limit) |
Equ. 1 |
Equ. 2 |
| Two Sided (Upper and Lower Limits) |
Equ. 3 |
Equ. 4 |
T = total accumulated unit-hours
r = total number of failures
α = acceptable risk of error
1 - α = confidence level