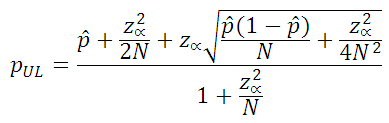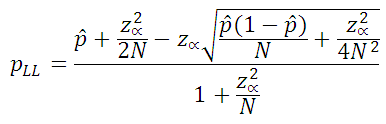
Two-sided confidence, exact method (N<=100)
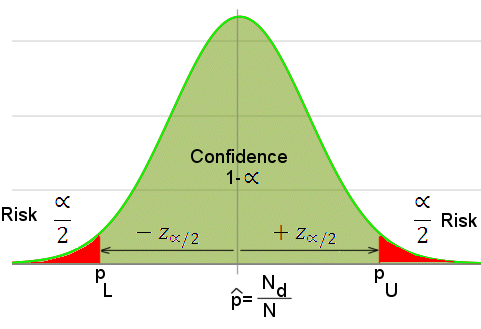
For sample sizes of 100 or less, the binomial exact method (Ref. 1) is used for calculating confidence intervals.
Given inputs of sample size (N), the number of defects found (Nd) and risk (α), which is one minus confidence, this tool iteratively seeks a solution by varying pU,
the upper confidence level for the proportion defective (p) in the left side of the equation, until the left and right sides are equal. The point estimate for the proportion defective is p=Nd/N.
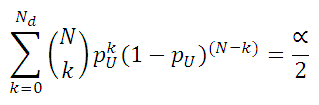
The following equation is solved for pL to obtain the to obtain the lower two-sided confidence level:
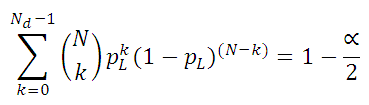
One-sided confidence, exact method (N<=100)
The calculation method for single sided limits are nearly identical to above, except all the risk is in either the upper or lower tail of the distribution. Therefore, α/2 is multiplied by two,
to represent all risk being in only one tail of the distribution.
The following equations are solved iteratively to determine the single-sided upper confidence limit (pU) or single-sided lower confidence limit (pL):
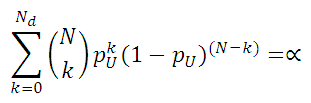
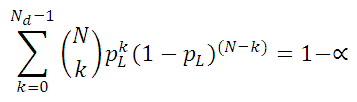
Two-sided confidence, Wilson method (N>100)
The following two equations (Ref. 1) are used to calculate the two sided confidence levels for cases where the sample size is greater than 100.
z is the variate value from the standard normal distribution such that, for two-sided confidence intervals, area in each tail of the standard normal distribution is α/2.
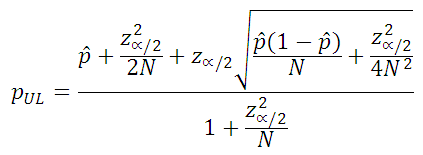
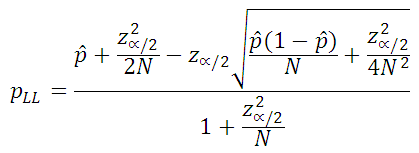
One-sided confidence, Wilson method (N>100)
To calculate single sided upper or lower confidence for cases where the sample size is greater than 100, the following two equations are used,
which are only different than the above equations in that z is not divided by 2, thereby representing all probability in only one tail of the distribution.
Toolkit Home
Comments/Questions:
reliabilityanalytics.com